同事介绍负载均衡算法时透露，其原B站leader透露说B站的负载均衡算法是基于一篇对扔球进桶问题讨论的论文。正好笔者曾看过相关内容，也深感这一简单的概率游戏有着让人意外的结果，故希望写一系列的文章，介绍这一简单而优美的结果。（本文首发于腾讯云+社区。）

在服务器的负载均衡模型中，我们可以把负载均衡看作是“扔球进桶”的游戏——我们的目标即最小化含有球数量最高的桶里的球的数量。在讨论中，有三种模型：

• 静态模型：把球一个一个地扔进桶里（扔第$i$个球时，前$i-1$个球被扔进了哪里是已经确定的）；
• 并行化模型：所有的球同时扔进桶里（扔球没有顺序关系）；
• 动态模型：球按一定规律随时间到来，每个桶按一定的速度消耗掉球。

其中，动态模型最接近真实情况。为简便起见，我们将在本系列文章中详细讨论把$n$个球扔进$n$个桶的静态模型，并介绍更接近于真实负载均衡场景的静态模型中球数多项式倍于桶数的情况与其他模型的结论。

我们希望详细讨论的问题有两个：

1. 完全随机地扔$n$个球进$n$个桶里，最后球最多的桶里的球数的期望是多少？
2. 扔$n$个球进$n$个桶里，每次完全随机地挑两个桶，把球扔进球数较少的桶里，最后的结果有怎样的改变？

一、远离期望

意料之外与情理之中：生日问题

假设所有人的生日为365天之中的其中一天，且机会均等。

1. 当优图实验室有多少人时，我们可以保证有两人的生日是在同一天？

2. 随机选取$n$人，估计这$n$人中存在两人生日是在同一天的概率大致是以下数字中的哪一个：

   \[0.01\%, 1\%, 5\%, 25\%, 50\%, 90\%, 99.9999\%\]
   • $n = 7$
   • $n = 23$
   • $n = 60$
   • $n = 183$

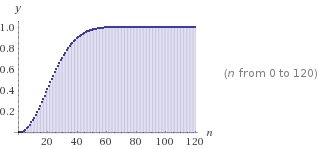
对于第一题，根据鸽笼原理，答案是$366$人。 对于第二题，结果可能出人意料：

• $n = 7,\ 5.23\%$
• $n = 23,\ 50.72\%$
• $n = 60,\ 99.41\%$
• $n = 183,\ \sim 1-{10}^{24}$

其计算方法是：

当有$n$人时，不存在两人生日在同一天的情况有 $b(n) = {365 \choose n} \cdot n!$ 种，而$n$人生日的所有情况有$365^n$种。因此，存在两人生日在同一天的“概率”为：

\(\Pr(\textrm{ex. 2 people who have the same birthday}) = 1-b(n)/365^n,\) 可画出图如下：

随机变量、期望，以及远离期望

在本节中，我们将介绍概率论中的几个基本概念，以及在讨论中会使用到的几个不等式。在讨论中，我们都以扔硬币游戏为例。

在这里我们不严格定义概率和概率空间；我们可以称“概率”，是指样本空间$\Omega$（随机过程中可能的结果）中允许的“事件”由概率函数$\Pr$得到的数值；这里，概率函数的值域为1，且$\Pr(\Omega) = 1$，且对于彼此独立的事件$E_1, \dots$有$\Pr(\cup_{i\geq 1} E_i) = \sum_{i \geq 1} \Pr(E_i)$。

例如扔一枚均匀的硬币，样本空间为$\Omega = {\textrm{Head, Tail}}$，允许的事件即为正面朝上（Head）与反面朝上（Tail），而概率函数选择为：

\[\Pr(E) = \begin{cases}0.5,\qquad E = \textrm{Head,}\\ 0.5, \qquad E = \textrm{Tail.} \end{cases}\]

随机变量

随机变量$X$是将样本空间映射到实数值的函数，即$X: \Omega \to R$. 与概率函数不同，随机变量无需具有概率函数的三性质。

例如，在扔硬币游戏中，我们定义$X$为：

\[X = \begin{cases}1,\qquad E = \textrm{Head},\\0, \qquad E = \textrm{Tail}.\end{cases}\]

该随机变量即描述了扔一枚均匀的硬币，扔出正面获得$1$元，否则获得$0$元的规则。

数学期望

假设扔一枚均匀的硬币，扔出正面获得$1$元，否则获得$0$元。玩一次该游戏，我们期望能有多少受益？

我们的直观告诉我们，我们期望收益是$0.5$元。

随机变量$X$的数学期望也是按这样的思路定义：

$E[X] = \sum_i i\cdot \Pr(X = i)$.

因此我们可以计算，玩一次扔硬币游戏的期望是：

$E[X] = 1\times 0.5 + 0\times 0.5 = 0.5$.

容易证明，数学期望具有线性，即$E[aX + bY] = aE[X] + bE[Y]$.

远离数学期望的概率

我们继续扔硬币游戏，假设连续玩$n$次（其随机变量分别定义为$X_1, \dots, X_n$），我们定义$X = X_1 + \dots + X_n$，则$X$的期望是多少？

$E[X] = E[\sum_{i=1}^n X_i] = \sum_{i=1}^n E[X_i] = 0.5n$.

但是仍然有可能，我们的收益远少于$0.5n$（例如连续扔出$n$次反面），因此我们想要限制随机变量的值远离其期望的概率。

马尔科夫不等式（Markov Inequality）

对于取值非负的随机变量$X$，对于任意的$a>0$，有 \(\Pr(X\geq a)\leq E[X]/a.\)

证明：

当$a > 0$，令 \(I=\begin{cases}1,\qquad X\geq a\\ 0,\qquad \textrm{otherwise.}\end{cases}\)

则根据$I$的定义，有$I \leq X/a$。

于是我们有 \(E[I] = \Pr[I = 1]=\sum_{i\geq a}\Pr[X = i]\leq \sum_{i\geq a}\Pr[X = i]\cdot \frac i a = E[X/a] = E[X]/a.\)

切比雪夫不等式（Chebyshev’s Inequality）

方差

我们定义方差$\textrm{Var}[X] = E[(X - E[X])^2]$.

直观地看，一个随机变量越可能远离其期望，其方差越大。

切比雪夫不等式

对于任意的$a > 0$， \(\Pr[|X-E[X]| \geq a] \leq \textrm{Var}[X]/a^2.\)

即，随机变量远离其期望超过$a$的概率，随方差线性增加，随 $a$ 二次减少。

证明：

\(\Pr(|X - E[X]| \geq a) = \Pr((X - E[X])^2 \geq a^2).\) 利用马尔科夫不等式，有

\[\Pr((X - E[X])^2 \geq a^2) \leq E[(X - E[X])^2] / a^2 = \textrm{Var}[X] / a^2.\]

切尔诺夫上界（Chernoff’s bound）

以上两个不等式都是关于一个随机变量的，现在对于多个随机变量（例如连续扔多次硬编的游戏），我们可以限制其远离期望的概率。

切尔诺夫上界可以被描述为：

令$X_1, \dots, X_n$为独立的泊松实验¹，其满足$\Pr(X_i = 1) = p_i$. 令$X = \sum_{i = 1}^n X_i$且$\mu = E[X].$ 则对于任意的$\delta > 0$， \(\Pr\left(X\geq\left(1+\delta\right)\mu\right)\leq{\left(\frac{e^\delta}{{\left(1+\delta\right)}^{\left(1+\delta\right)}}\right)}^\mu.\)

切尔诺夫上界证明了，对于一连串的泊松实验，其结果之和远离其期望的概率会关于远离幅度（$\delta$）和期望大小（$\mu$）指数地下降。

切尔诺夫上界的证明利用矩母函数（moment generation functions）及其马尔科夫不等式。因时间有限，故在此省略；可参考证明。

切尔诺夫上界的特殊情况

对于服从成功概率为$p$的伯努利分布（成功则取值$1$，否则取值为$0$；例如，我们定义的扔硬币即服从成功概率为$0.5$的伯努利分布）的一系列随机变量$X_1, \dots, X_n$，定义$X = \sum_{i = 1}^n X_i$，$\mu = E[X]$，则对于任意的$0 < \delta \leq 1$，有

\[\Pr[X \geq (1 + \delta)\mu] \leq e^{-\mu\delta^2/3};\]

对于任意的$R>6\mu$，有

\[\Pr[X \geq R] \leq 2^{-R}.\]

（该二者均可通过原切尔诺夫上界推导出；过程在此省略。）

例如，连续玩2000次扔硬币游戏，最终收益超过1250元（$\delta = 0.25$）的概率不超过$e^{-1000\times0.25^2/3} <8.96\times 10^{-10}$，该值大约是随机地买一注双色球彩票中一等奖概率的$\frac 1 {63}$。

---

在本章中我们讨论了关于概率的基本概念，并通过马尔科夫不等式、切比雪夫不等式和切尔诺夫上界知道了随机变量取值远离其期望的概率。有了基本的概念和数学工具，我们将在下一章讨论完全随机地扔$n$个球进$n$个桶里，最后球最多的桶里的球数的期望。

二、闭着眼睛选一个

上一章我们以扔硬币为例介绍了概率论中的基本概念，并且证明了本系列文章需要的三个不等式。有了这些基本内容，我们将在本章讨论完全随机地扔$n$个球进$n$个桶里，最后球最多的桶里的球数的期望。

我们希望限制球数最大的桶的球数，这里我们证明：

球数最大的桶的球数的期望为$\Omega(\frac {\ln n} {\ln\ln n})$。

我们分两个步骤证明：

• （期望的上界）存在球数不小于$\frac {3\ln n} {\ln\ln n}$的桶的概率不超过$\frac 1 n$；
• （期望的下界）存在球数超过$\frac {\ln n} {3\ln\ln n}$的桶的概率超过$1 - \frac 1 {n^{2/3}}$。

上界的证明

限制桶$i$球数太大的概率

利用切尔诺夫上界，这里我们知道对于任意的桶$B_i$，设随机指示器（事件发生时取值为$1$、否则为$0$的随机变量）

\[X_j^{B_i} = \begin{cases}1, \qquad \text{球}j\text{被扔进}B_i,\\0, \qquad \text{otherwise.}\end{cases}\]

这里$X_j^{B_i}$可以看成是以概率为$1/n$的伯努利实验的结果；取$X^{B_i} = \sum_{j=0}^n X_j^{B_i}$，则$E[X^{B_i}] = 1$，利用切尔诺夫上界，这里令$\delta = \frac {3\ln n}{\ln\ln n} - 1$，记$b = \delta + 1 = \frac {3\ln n} {\ln\ln n}$，有

\[\Pr(E[X^{B_i}] > b + 1) \leq \frac {e^{b-1}}{b^b} = \frac 1 e(\frac e b)^b = \frac 1 e (\frac {e\ln\ln n}{3\ln n})^b \leq \frac 1 e (\frac{\ln\ln n}{\ln n})^b,\]

这里分别有$e^b = n^{3/\ln\ln n}$ ²，因为$(\ln\ln n )^b = e^{b\ln\ln\ln n} = n^{3\ln\ln\ln n / \ln\ln n},$

所以$(\ln n)^b = (\ln n)^{\frac {3\ln n }{\ln\ln n}} = e^{\frac {3\ln n \ln\ln n}{\ln\ln n}} = e^{3\ln n} = n^3$ ³，因此$\Pr(E[X^{B_i}] > b + 1) \leq \frac 1 e n^{\frac {3\ln\ln\ln n}{\ln\ln n} - 3}\leq \frac 1 {en^2} \leq 1 / n^2.$

Union Bound

这里我们引入Union Bound（也称布尔不等式，Boole’s inequality）。该不等式描述的含义为，一系列事件中至少发生一个的概率不超过其单个事件的概率之和。例如，随机从54张牌中抽5张牌，“其中有一对4或者一对9”的概率小于“其中有一对4”的概率加“其中有一对9”的概率——这是因为后者计算了两次“其中有一对4且其中有一对9”。

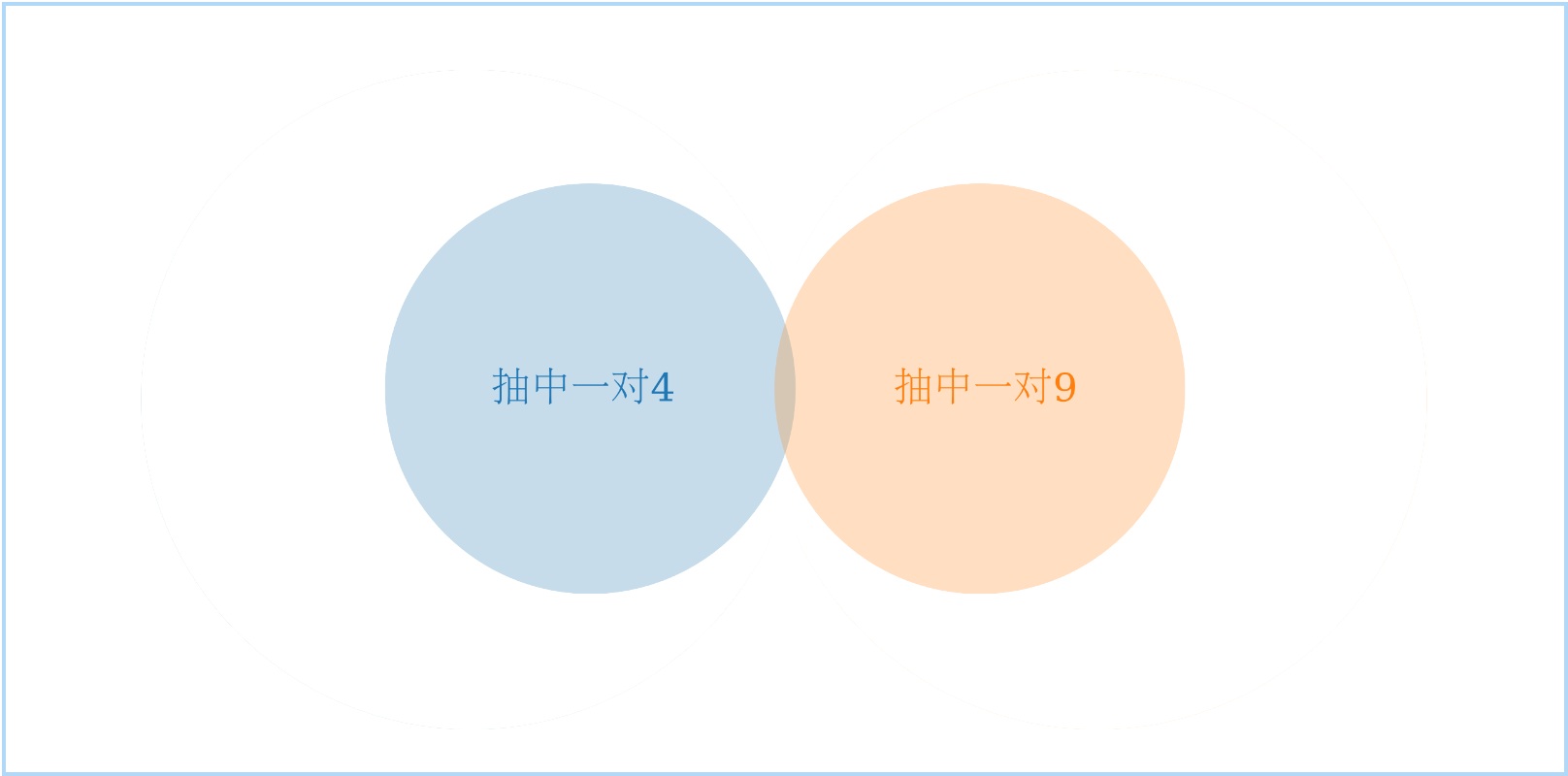
正式的表述为：$\Pr(\cup_i X_i) \leq \sum_i\Pr(X_i).$

存在球数太大的桶的概率

我们利用第一小节的结论，即，对于任意的$i\in[n]$，桶$i$的球数超过$\frac {3\ln n} {\ln\ln n}$的概率不超过$1/n^2$，使用第二小节提到的Union Bound，有：

存在球数超过$\frac {3\ln n} {\ln\ln n}$的桶的概率不超过$\sum_{i = 1}^n 1/n^2 = 1/n.$

球最多的桶的球数的期望的上界

这里我们令$X$代表球最多的桶的球数，令

\[X' = \begin{cases}\frac {3\ln n} {\ln\ln n}, \qquad X\leq\frac {3\ln n} {\ln\ln n}, \\ n, \qquad\qquad\textrm{otherwise}. \end{cases}\]

显然有$X \leq X’$，因为$X$至多取值到$n.$ 因此，

\[E[X] \leq E[X'] \leq \frac {3\ln n} {\ln\ln n}\cdot (1 - 1/n) + n \cdot 1/n \leq \frac {3\ln n} {\ln\ln n} + 1.\]

下界的证明

首先我们设随机指示器变量$X_i$，其值取$1$当且仅当桶$i$的球数不小于$k$（稍后我们确定$k$的值）。则有

$\Pr(X_i = 1) \geq \frac {n \choose k} {n^k}.$

这是因为该桶球数不小于$k$的扔球方法里，包括随机选$k$个球扔进该桶$n\choose k$种情况，而这$k$个球的扔法有$n^k$中情况。

由于对于$n \geq k > i$，有$\frac {n-i}{k-i} \geq \frac n k$，故有${n \choose k} \geq {(\frac n k)}^k$，因此$\Pr(X_i = 1) \geq 1/k^k.$

这里我们取$k = \frac {\ln n}{3\ln\ln n}.$

于是有$1/k^k = (n^{-1 + \frac {\ln\ln\ln n - \ln\ln n}{\ln n}})^{\frac 1 3} = 1/\sqrt[3+\varepsilon]n$（计算过程略，与上文的过程类似）；这里$\lim_{n\to\infty}\varepsilon = 0.$

则我们有$E[X_i] \geq 1/\sqrt[3+\varepsilon]n.$

记$X = \sum_{i\in[n]}X_i$，则有$E[X] \geq n^{\frac 2 3-\varepsilon}.$

即，所有桶中我们期望有$n^{\frac 2 3 - \varepsilon}$个桶球数较多。但这并不能证明，$\Pr(X\geq 1) \to 1$，即存在一个桶的球数较多这件事一定会发生。反例：考虑另一随机变量$Y$，它有$1/n^{\frac 1 3}$的概率取值为$n$，其余情况取值为$0$，则我们有$E[Y] = n\cdot 1/n^{\frac 1 3} = n^{\frac 2 3}.$ 但是随着$n$增大，$\Pr(Y\geq 1) \to 0.$

因此我们需要用到「二阶矩」的分析。这里我们回忆「方差」的概念，对于$\textrm{Var}[X + Y] = \textrm{Var}[X] + \textrm{Var}[Y] + \textrm{Cov}[X, Y].$ 这里$\textrm{Cov}[X, Y]$为随机变量$X, Y$的协方差，其定义为：$\textrm{Cov}[X, Y] = E[(X - E[X])\cdot (Y - E[Y])] = E[XY] - E[X]E[Y].$ 这里我们看到，如果一个随机变量在大于其期望的时候另一个也大于其期望，则协方差为正，否则为负。

回到我们的论述，我们现在可以得到$\textrm{Var}[X] = \sum_{i\in [n]}\textrm{Var}[X_i] + \sum_{i \neq j}\textrm{Cov}[X_i, X_j].$ 这里，我们的直观告诉我们，桶$i$球数较多时，会隐含着桶$j$的球数不会太多，因为两个不同的桶在“争抢”固定的球。因此，$X_i$在大于其期望，即取值为$1$时，$X_j$会更可能小于其期望，即取值为$0$。故，$\textrm{Var}[X] \leq \sum_{i\in[n]}\textrm{Var}[X_i].$

而此时，$\textrm{Var}[X_i] = E[X_i^2] - E[X_i]^2$，由于$X_i$是随机指示器变量，故$E[X_i^2] = E[X_i]$，因此$\textrm{Var}[X_i] \leq E[X_i].$

利用切比雪夫不等式，记$\mu = E[X] \geq n^{\frac 2 3-\varepsilon}$，有

\[\Pr(X = 0) \leq \Pr(|X - \mu|\leq \mu) \leq \frac {\textrm{Var}[X]} {\mu^2} \leq \frac {\sum_{i\in[n]}\textrm{Var}[X_i]} {\mu^2}\leq \frac {n^{2/3 - \varepsilon}}{\mu^2} \leq 1/n^{2/3}.\]

因此$\Pr(X \geq 1) = 1 - \Pr(X = 0) \geq 1 - n^{2/3}.$

故，我们扔完$n$个球后，以很高的概率会有存在球数达到$\frac {\ln n} {3\ln\ln n}$的桶。

利用与上文类似的分析桶最大球数期望的方法我们可以知道该期望的下界为$\frac {\ln n} {3\ln\ln n} - 1.$

经过分析我们发现，完全随机地向$n$个桶里扔$n$个球，最后球最多的桶的球数之期望为$\Omega(\frac {\ln n} {\ln\ln n})$，并且以很高的概率，该数值在$\frac {\ln n} {3\ln\ln n}$到$\frac {3\ln n} {\ln\ln n}$之间。

这个结论是出人意料的，因为我们知道每个桶里球数的期望其实是$1$，而这里最大负载很大概率居然是期望的$\Omega(\frac {\ln n} {\ln\ln n})$倍！

这告诉我们在负载均衡场景中，单纯使用随机的方法分配请求是不够好的。那么我们能否做得更好？接下来我们继续深入。

三、选两个，再瞅一眼！

在上一章中我们讨论了随机地把$n$个球扔进$n$个桶里后负载最大的桶的球数的期望——$\Omega(\frac {\ln n } {\ln\ln n})$；在本章中，我们将讨论一个看似微小的改进：每次随机选择两个桶，把球扔进这两个桶中负载最小的桶里；我们将说明，最终负载最大的桶的球数的期望将有指数级的下降。

仅仅多挑一个桶，结果就有指数级的下降——实际上，每次随机选$d$个桶，把球扔进这两个桶中负载最小的桶里，最终的最大负载以很高的概率不会超过$\frac {\ln\ln n} {\ln d} + O(1)$；证明可以参考Michael Mitzenmacher的博士论文的第1.2节；由于证明需要非常细致地对条件概率进行处理，我们在本章中仅介绍证明的思路，且限制$d = 2$。

准备工作

我们将定义如下术语：

• 在时刻$t$：刚扔出第$t$个球时；
• 时刻$t$前：扔完第$t-1$个球后，扔第$t$个球之前
• 时刻$t$后：刚扔出第$t$个球后；
• $\omega_t$：$t$时刻扔出的球所落的桶；这里，$(\omega_1, \dots, \omega_n)$决定了整个扔球过程；
• 球的高度：球被扔进桶里时，除该球外桶里的球的数量加$1$；
• 记$\beta_i$表示在时刻$n$后球数超过$i$的桶的数量的上界。

我们将定义如下随机变量：

• $\#Bin_i(t)$表示时刻$t$后负载不小于$i$的桶的数量；
• $\#Ball_i(t)$表示时刻$t$后高度不小于$i$的球的数量。

显然，负载不小于$i$的桶里至少存在$1$个高度为$i$的球，故$\#Ball_i(t) \geq \#Bin_i (t).$

证明思路

我们利用$\beta_1, \dots, \beta_k$来限制负载过大的桶的数量，而这些值我们通过归纳法得到——当我们扔出一个高度不小于$i+1$的球的时候，一定是随机挑到了两个负载不小于$i$的桶。

利用归纳法，当$\#Bin_i(n) \leq \beta_i$时，在扔任意球的时候我们都有：扔出该球的高度大于$i$的概率最多为：$p_i = (\frac {\beta_i} n)^2.$ 因此在整个过程中，高度大于$i$的球的数量的期望最多为$np_i$。于是，我们可以设$\beta_{i + 1} = np_i = \frac {\beta_i^2} n.$

我们可以以某个$i$开始限制$\beta_i$，例如我们有$\beta_2\leq n/2$（鸽笼原理）。现在递推，可以知道$\beta_{i + 2} = \frac n {2^{2^i}}.$

因此，设$i = \log\log n + O(1)$，有$\beta_{i + 2} < 1.$

这样就证明了数量超过$\log\log n$的桶的数量的期望小于1。

多看一眼的神奇之处

为什么每次从闭着眼睛随机选一个桶来扔球，到每次挑选两个桶扔进负载较小的一个桶里，我们的最大负载有了指数级的下降？答案当然可以是：详见证明。但真正给我们的直观是，多了关于桶负载的“信息”——这也能某种程度上说明，每次挑选$d$个桶时，$d = 1$和$d = 2$有本质的区别（指数倍下降），而$d = 2$和$d = O(1)$没有本质的区别（常数倍下降）。

指数级的负载下降。那么，我的朋友，代价是什么呢？

$d = 1$与$d > 1$的区别是RTT，球需要发起一轮询问并接收一轮消息。信息的传递使得最终的负载有了指数级的下降。

四、进一步的结论

我们已经讨论了静态模型（逐个地扔球进桶）中扔$n$个球进$n$个桶的情况，每次随机挑两个桶的方法比起完全随机扔球会有指数级的最大负载下降。在本章中我们会介绍当球数远大于桶数时的结果，以及其他模型下的结论。

在本章的讨论中，我们记球数为$m$，记桶数为$n.$

静态模型下随机扔$m » n$个球

在前两章的讨论中，为了分析的简便，我们都是假设$m = n$；证明也可以容易地扩展到$m = n\log n$的情况。但当球数多项式倍于桶数的时候，即$m = \textrm{poly}(n)$时，证明将变得复杂起来——而这恰恰是负载均衡话题中通常会讨论到的情况——请求数量远多于服务器的数量。

我们下面介绍Raab和Steger关于完全随机扔球进桶的工作和Berenbrink等人在STOC 2000的工作；Talwar和Wieder在ICALP 2014给出了与后者同样的结论但证明更简化的版本。

在我们的模型中，我们定义随机变量$Gap$为扔完$m$个球进$n$个桶后，负载最大的桶的球数与桶里球数的期望之差。例如，我们前两章讨论的$n = m$结果，对于完全随机扔球进桶，$E[Gap] = \Omega(\frac {\ln n } {\ln\ln n}) - 1 = \Omega(\frac {\ln n } {\ln\ln n})$；而随机挑两个桶扔进负载较小的桶里，我们有$E[Gap] = \Omega(\ln\ln n) - 1 = \Omega(\ln\ln n).$

Raab和Steger证明了，对于$m > \frac n {\textrm{polylog}(n)}$，完全随机扔球进桶的情况是以很高的概率：

\[Gap = \Omega(\sqrt{\frac {m\log n}{n}}).\]

而Berenbrink等人证明了，对于任意的$m$，每次随机选$d>1$个桶并扔球进负载较低的桶里，有：

\[E[Gap] \leq \frac {\log\log n}{\log d} + O(\log\log\log n).\]

注意，这里每次挑两个桶的$Gap$的期望与球数不再相关！即使$m = 2^n$，最后$Gap$的期望也仍然只有$O(\log\log n)$！

动态模型

现在我们考虑这样的“超市模型”（supermarket model）——超市有$n$个收银台，每个收银台给顾客结账的时间服从均值为$1$的指数分布，顾客的到来服从参数为$\lambda n$的泊松过程（$0 < \lambda < 1$）（可以简单理解为任意两个顾客到达收银台的间隔的期望是$\frac 1 {\lambda n}$，即每单位时间收银台前会新增$\lambda n$个顾客），每个收银台遵循FIFO的规则为顾客结账。假设每个顾客抵达收银台时随机选择$d$个收银台，并前往其中负载最小的收银台排队等候。如图，顾客A选择随机选两条队列，然后排到其中长度较小的那一个中；顾客B刚被服务，已经离开收银台。

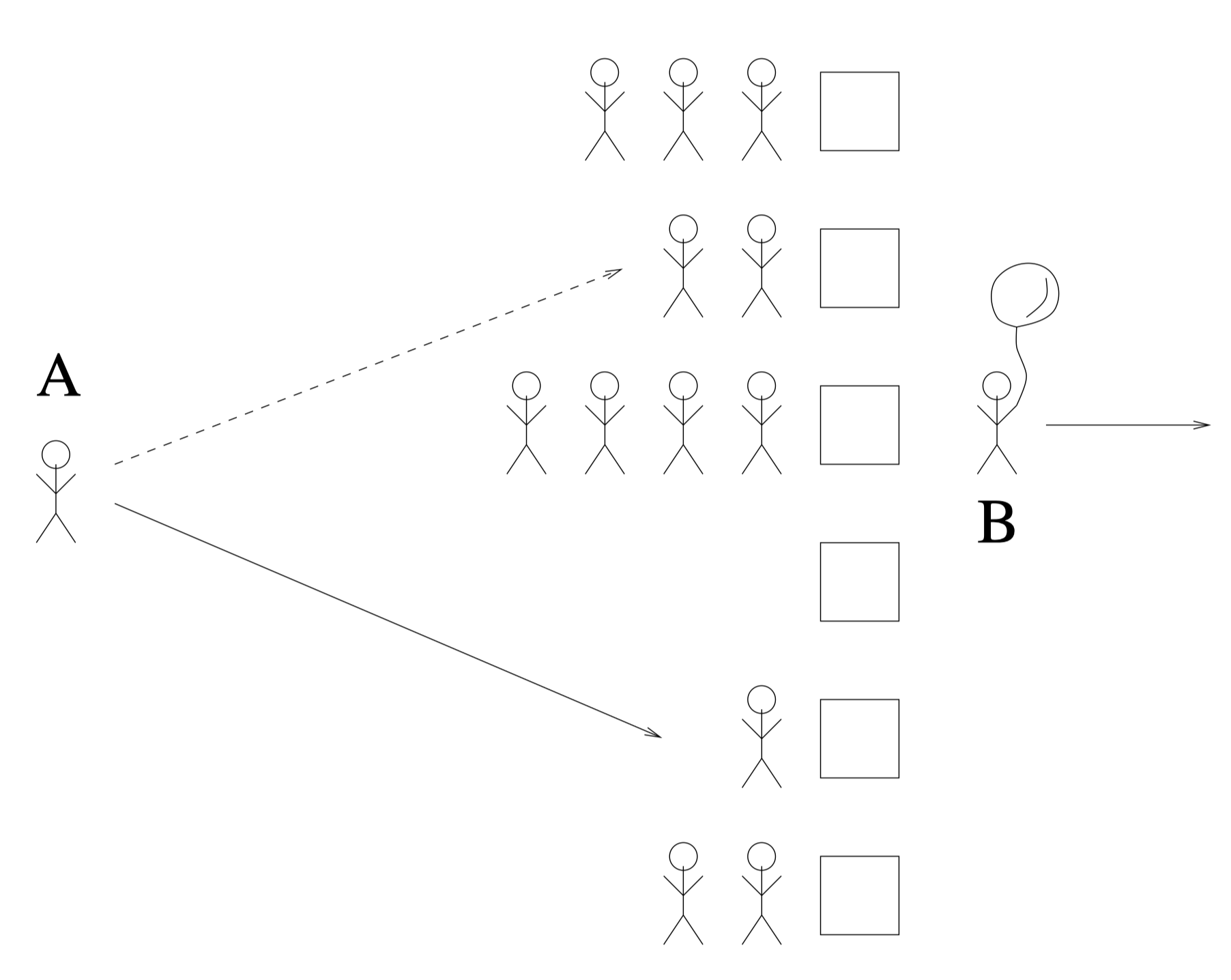
这一超市模型在某种程度上符合现实中的负载均衡情况。Michael Mitzenmacher在其博士论文中讨论了该情况，由于分析十分复杂，我们也仅介绍结论：

队列初始都为空的情况下，对于任意的$T > 0$，对于$d>2$，在时间段$[0, T]$中队伍长度的最大值以很高的概率为$\frac {\log\log n} {\log d} + O(1).$

即，我们在动态模型中得到了静态模型类似的结论，只要该过程每时刻到达收银台的顾客数的期望不超过收银台的数量，那么任意时间段内队伍的最大长度都只会是$\Omega(\log\log n)$！

甚至我们可以扩展：高优先级的请求（出现概率为$p$）随机挑两个服务器并进入负载较低的服务器排队，而低优先级的请求（出现概率为$1-p$）完全随机地挑选一个服务器；请求的出现仍然服从参数为$\lambda n$的泊松过程，在$\lambda = 0.99$时我们可以画出图像：

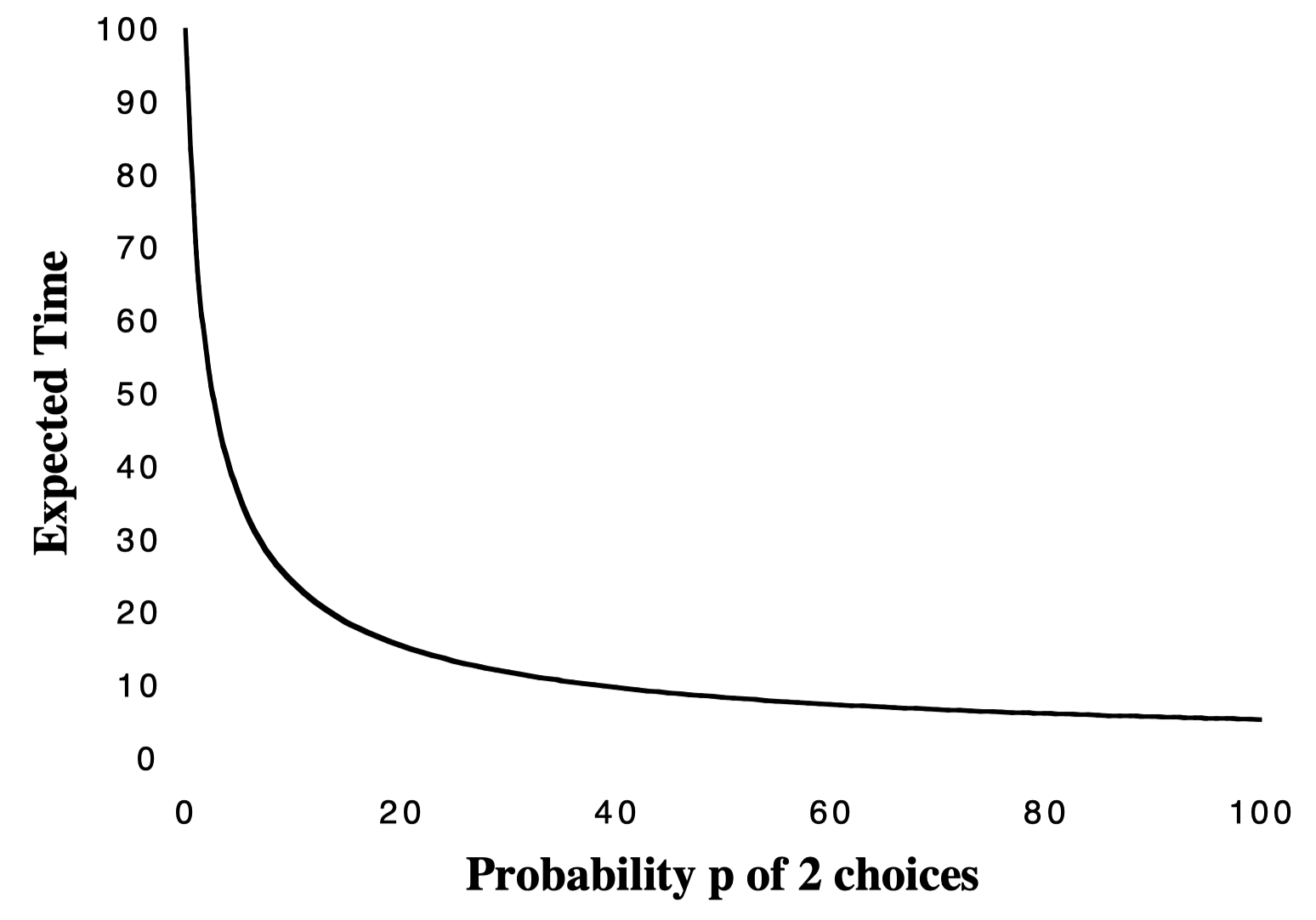
可以看见，只要有一小部分任务“选两个再多瞅一眼”，就能显著降低队列长度的期望。

总结

我们在这一系列的文章中介绍了概率的几个基本概念与基本不等式，并应用它们尝试解决扔$n$个球进$n$个桶游戏中最大负载的桶的球数的期望，我们发现：每次随机挑选两个桶并将球扔进负载较低的桶里，比起完全随机挑选一个桶再扔进去有了指数级的负载降低，即从$\Omega(\frac {\log n} {\log\log n})$降低到$O(\log\log n).$ 我们进一步介绍了当球数远多于桶数时，随机挑两个的结果使得最大负载与平均负载的差值（$Gap$）与球数不再相关，以及动态模型中随机挑两个的策略也可以得到和静态模型中相似的结果。

我们认为其背后的哲学在于，随机挑两个球的模型是因为其知道了桶里球分布的信息，使得最终结果有了指数级的提升。但其代价在于，信息的传递需要时间。在最后我们也介绍了，只有一部分球随机选两个的动态模型，最终的结果也能有很大的提升。

当然在现实中我们不期望负载均衡是完全符合我们的假设，例如请求的到来服从泊松分布、每台服务器的性能相同、每个请求的完成时间的期望相同，但是对于这样理论情况的分析还是可以一定程度上指导我们的算法。希望这一系列的文章对你有所帮助。

感谢阅读！

参考文献

• Mitzenmacher M, Upfal E. Probability and computing: Randomization and probabilistic techniques in algorithms and data analysis. Cambridge university press, 2017.
• Gupta A. Lec 8: Balls and Bins/Two Choices, Lecture Notes, 15-859M: Randomized Algorithms, Carnegie Mellon University.
• Mitzenmacher, Michael David. The power of two random choices in randomized load balancing. Diss. PhD thesis, Graduate Division of the University of California at Berkley, 1996.
• Berenbrink, Petra, et al. “Balanced allocations: the heavily loaded case.” Proceedings of the thirty-second annual ACM symposium on Theory of computing. 2000.
• Talwar, Kunal, and Udi Wieder. “Balanced allocations: A simple proof for the heavily loaded case.” International Colloquium on Automata, Languages, and Programming. Springer, Berlin, Heidelberg, 2014.
• Raab, Martin, and Angelika Steger. “Balls into bins”—A simple and tight analysis. International Workshop on Randomization and Approximation Techniques in Computer Science. Springer, Berlin, Heidelberg, 1998.
• Richa, Andrea W., M. Mitzenmacher, and R. Sitaraman. “The power of two random choices: A survey of techniques and results.” Combinatorial Optimization 9 (2001): 255-304.